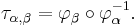Atlas (topology)

For other uses of "atlas", see Atlas (disambiguation).

In mathematics, particularly topology, one describes a manifold using an atlas. An atlas consists of individual charts that, roughly speaking, describe individual regions of the manifold. If the manifold is the surface of the Earth, then an atlas has its more common meaning. In general, the notion of atlas underlies the formal definition of a manifold.

Contents

Charts

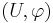The definition of an atlas depends on the notion of a chart. A chart for a topological space M is a homeomorphism \varphi from an open subset U of M to an open subset of Euclidean space. The chart is traditionally recorded as the ordered pair (U, \varphi).

Formal defintion of atlas

An atlas for a topological space M is a collection 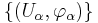\{(U_{\alpha}, \varphi_{\alpha})\} of charts on M such that 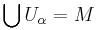\bigcup U_{\alpha} = M. If the range of each chart is the n-dimensional Euclidean space, then M is said to be an n-dimensional manifold.

Transition maps

A transition map provides a way of comparing two charts of an atlas. To make this comparison, we consider the composition of one chart with the inverse of the other. This composition is not well-defined unless we restrict both charts to the intersection of their domains of definition. (For example, if we have a chart of Europe and a chart of Russia, then we can compare these two charts on their overlap, namely the European part of Russia.)

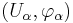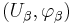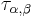To be more precise, suppose that (U_{\alpha}, \varphi_{\alpha}) and (U_{\beta}, \varphi_{\beta}) are two charts for a manifold M such that U_{\alpha} \cap U_{\beta} is non-empty. The transition map \tau_{\alpha,\beta} is the map defined on the intersection U_{\alpha} \cap U_{\beta} by

\tau_{\alpha,\beta} = \varphi_{\beta} \circ \varphi_{\alpha}^{-1}.

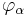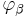Note that since \varphi_{\alpha} and \varphi_{\beta} are both homeomorphisms, the transition map 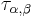\tau_{\alpha, \beta} is also a homeomorphism.

More structure

One often desires more structure on a manifold than simply the topological structure. For example, if one would like an unambiguous notion of differentiation of functions on a manifold, then it is necessary to construct an atlas whose transition functions are differentiable. Then one can unambiguously define the notion of tangent vectors and then directional derivatives.

If each transition function is a smooth map, then the atlas is called a smooth atlas. Alternatively, one could require that the transition maps have only k continuous derivatives in which case the atlas is said to be 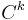C^k .

Very generally, if each transition function belongs to a pseudo-group 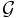{\mathcal G} of homeomorphisms of Euclidean space, then the atlas is called a 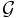{\mathcal G}-atlas.

References

  • Lee, John M. (2006). Introduction to Smooth Manifolds. Springer-Verlag. ISBN 978-0-387-95448-6. 
  • Sepanski, Mark R. (2007). Compact Lie Groups. Springer-Verlag. ISBN 978-0-387-30263-8. 

External links